Introduction
Accurate modeling of Gaussian beam propagation is essential in laser engineering for designing precise optical systems. Physical Optics Propagation (POP) offers a wave-based approach that captures diffraction, interference, and spatial filtering effects with high accuracy—unlike traditional ray-based methods. This article explores how POP enhances the analysis and optimization of Gaussian beam behavior across diverse optical configurations.
Physical Optics Propagation (POP)
Physical Optics Propagation (POP) is a powerful tool used to simulate the propagation of light waves. The beam is represented by an array of discretely sampled points, similar to ray tracing used in geometrical optics but with a more complex approach. This wavefront-based method allows a detailed analysis of beams, including Gaussian beams or other multi-mode beams. POP models the beam by tracking its electric field as it propagates through the optical system, capturing intricate effects like diffraction, spatial filtering, and beam shaping.
The strength of POP lies in its ability to handle beams that exhibit complex behavior, such as Gaussian beams, and analyze effects that ray tracing cannot address, like diffraction at the edges of lenses or apertures. This makes POP especially useful for systems where diffraction and beam shaping are critical.
Example: Modeling Gaussian Beam Propagation with POP
Let’s consider a scenario where we need to model the focusing of a Gaussian beam using a singlet lens. The beam has the following specifications:
- Nominal Wavelength: 355 nm
- Measured 5 mm from the laser output:
- Beam diameter: 2 mm
- Measured divergence: 9 mrad
Given this information, we can calculate the beam waist location and Rayleigh range for the Gaussian beam. The beam waist is determined using the known wavelength and divergence angle, and the Rayleigh range (which describes how the beam’s focus evolves) is calculated as 1.383 mm. The goal is to optimize the system so the beam is focused to the smallest spot size 100 mm from the laser output.
To model this in OpticStudio, we first start in the ray-based approach. A new surface is inserted after the object surface, and the object’s thickness is set to zero to ensure that the beam is launched correctly from the initial point.
- Beam Definition Settings:
- Beam Type: Gaussian Waist
- X/Y Sampling: 256×256
- Waist X/Y: 0.0125 mm
- Wavelength: 355 nm
- Rayleigh Range: 1.383 mm
- Results from Physical Optics Propagation: After optimizing the system, we achieve the smallest possible beam size of 9.94 um at the image plane. This refined value of the focused beam size is more accurate than those computed using traditional ray-based methods.
Optimization Using POP
The beam’s focal point is optimized by adjusting the lens configuration. Using POP, we can further refine the beam size at the image plane, adjusting the lens radii and beam parameters to achieve the most compact beam possible. The optimization results indicate that the smallest Gaussian beam size is approximately 9.44 um at 100 mm from the laser output, a slight improvement over the 9.45 um computed with the Paraxial Gaussian Beam analysis.
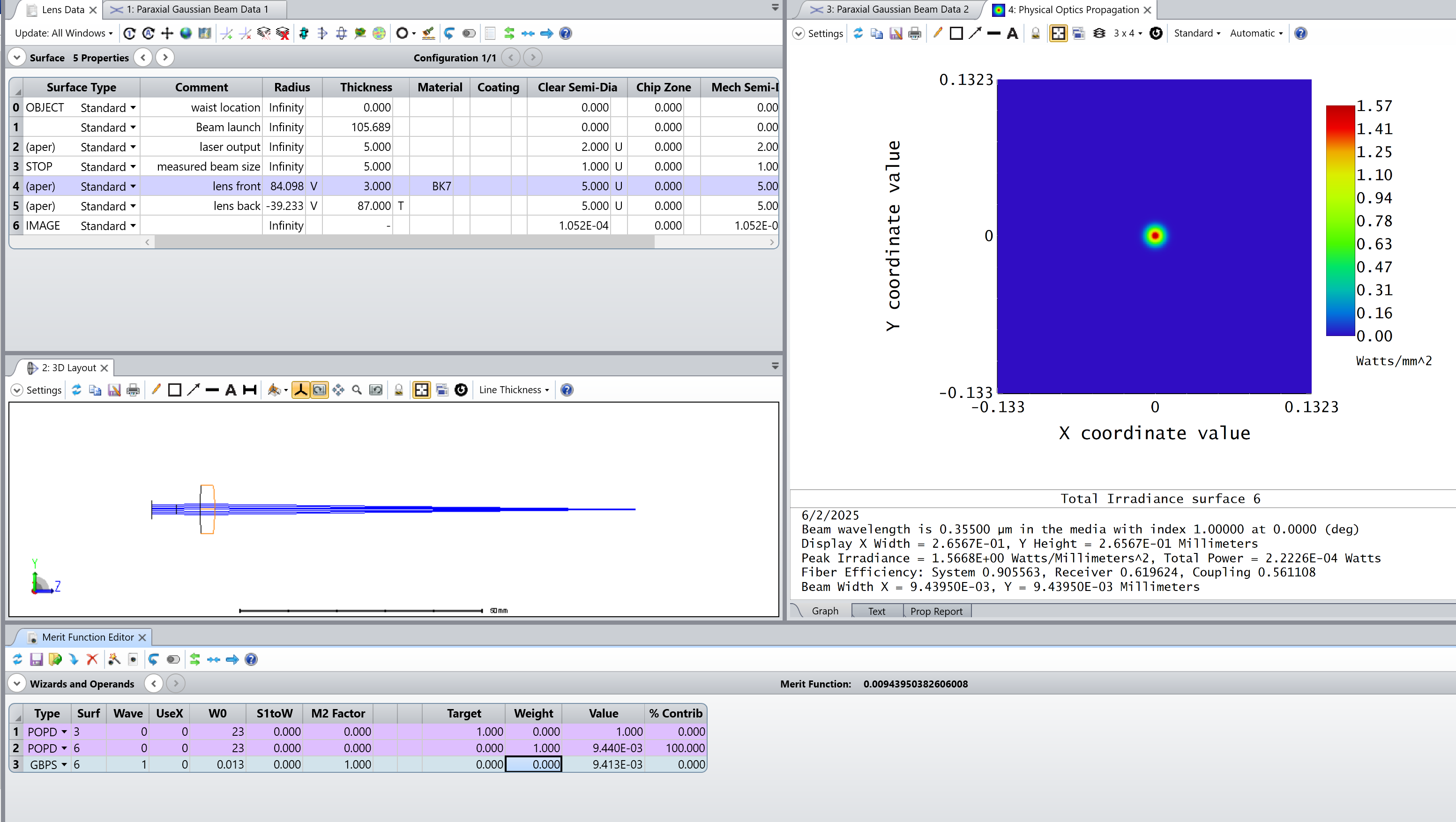
This example demonstrates the enhanced capabilities of Physical Optics Propagation for beam optimization in systems requiring precise control over beam divergence and spot size.
When to Use POP
POP is especially useful in scenarios where beam diffraction is significant and where ray-based methods fall short. Key scenarios include:
- Intermediate focus points where ray-based methods fail to predict the correct beam shape.
- Diffraction effects from focal regions or limited lens apertures.
- Long propagation distances where beam divergence becomes important and ray tracing does not accurately predict the beam’s behavior.
For Gaussian beams and other coherent light sources, Physical Optics Propagation provides a more accurate and robust solution for modeling beam behavior through optical systems.
Conclusion
In conclusion, Physical Optics Propagation is a powerful method for accurately modeling the propagation of Gaussian beams. By simulating the entire wavefront of the beam, POP allows for detailed analysis and optimization, especially when dealing with complex beam dynamics such as diffraction and beam shaping. Whether you’re designing lenses, optical fibers, or other systems requiring precise beam control, POP offers the accuracy needed to ensure optimal performance.





